मशीन लर्निंग में रिग्रेशन को समझें: प्रकार, अनुप्रयोग और लाभ

Regression एक सांख्यिकीय (Statistical) और मशीन लर्निंग (Machine Learning) तकनीक है, जिसका उपयोग निरंतर मान (Continuous Values) को प्रेडिक्ट (Predict) करने के लिए किया जाता है। यह सुपरवाइज्ड लर्निंग (Supervised Learning) का हिस्सा है, जहां मॉडल (Model) को इनपुट (Input) और आउटपुट (Output) के बीच संबंध (Relationship) सीखने के लिए लेबल्ड डेटा (Labeled Data) दिया जाता है। उदाहरण: घर की कीमत (House Price), तापमान (Temperature), या स्टॉक की कीमत (Stock Price) का अनुमान लगाना।

आइए, Regression को विस्तार से समझें:

1. Regression क्या है? (What is Regression?)

Regression का मुख्य लक्ष्य दो या दो से अधिक वेरिएबल्स (Variables) के बीच संबंध (Relationship) को समझना और एक निरंतर आउटपुट (Continuous Output) का अनुमान लगाना है।

Dependent Variable (टार्गेट): जिस मान को प्रेडिक्ट करना है (जैसे: घर की कीमत)।
Independent Variables (फीचर्स): जिन वेरिएबल्स का उपयोग प्रेडिक्शन के लिए किया जाता है (जैसे: घर का आकार, स्थान)।

2. Regression के प्रकार (Types of Regression)

2.1 Linear Regression (रैखिक प्रतिगमन)

इसमें Dependent और Independent Variables के बीच रैखिक संबंध (Linear Relationship) होता है।
Equation:
[
y = b_0 + b_1x_1 + b_2x_2 + \dots + b_nx_n
]
( y ): Dependent Variable
( x_1, x_2, \dots, x_n ): Independent Variables
( b_0 ): Intercept (अंत:खंड)
( b_1, b_2, \dots, b_n ): Coefficients (गुणांक)

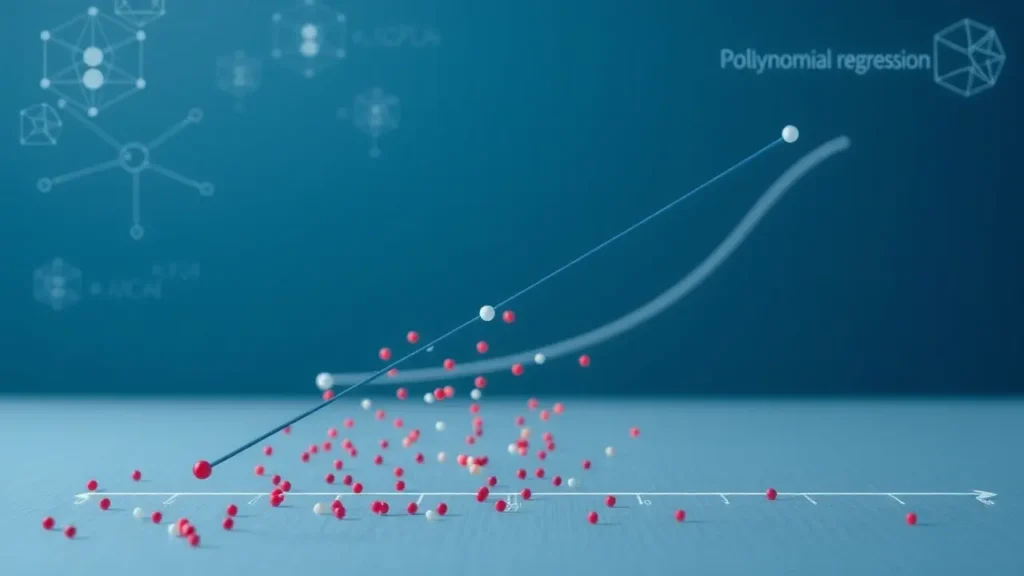
2.2 Polynomial Regression (बहुपद प्रतिगमन)

जब Variables के बीच संबंध रैखिक न होकर कर्व (Curve) के रूप में होता है।
Equation:
[
y = b_0 + b_1x + b_2x^2 + \dots + b_nx^n
]

2.3 Ridge Regression (रिज प्रतिगमन)

यह Overfitting को कम करने के लिए Linear Regression में L2 Regularization जोड़ता है।

2.4 Lasso Regression (लासो प्रतिगमन)

यह Overfitting को कम करने और Feature Selection के लिए L1 Regularization का उपयोग करता है।

2.5 Logistic Regression (लॉजिस्टिक प्रतिगमन)

इसे Classification के लिए इस्तेमाल किया जाता है, लेकिन नाम में “Regression” होने के बावजूद यह Probability (संभावना) को प्रेडिक्ट करता है।

3. Regression कैसे काम करता है? (How Does Regression Work?)

ट्रेनिंग डेटा (Training Data): मॉडल को इनपुट (Features) और आउटपुट (Target) वाला डेटा दिया जाता है।
लॉस फंक्शन (Loss Function): मॉडल के प्रेडिक्शन और Actual Value के बीच त्रुटि (Error) को मापा जाता है (जैसे: Mean Squared Error)।
ऑप्टिमाइजेशन (Optimization): Gradient Descent जैसे तरीकों से गुणांक (Coefficients) को ऑप्टिमाइज़ किया जाता है ताकि त्रुटि (Error) कम हो।
प्रेडिक्शन (Prediction): ट्रेन किए गए मॉडल का उपयोग नए डेटा पर प्रेडिक्शन के लिए किया जाता है।

4. Regression के उपयोग (Applications of Regression)

हेल्थकेयर (Healthcare): बीमारी के जोखिम का अनुमान (जैसे: Diabetes Risk Prediction)।
फाइनेंस (Finance): स्टॉक की कीमत या बाजार के रुझान का अनुमान।
मार्केटिंग (Marketing): विज्ञापन खर्च और बिक्री के बीच संबंध का विश्लेषण।
इंजीनियरिंग (Engineering): मशीनों के प्रदर्शन का अनुमान।

5. Regression के फायदे (Advantages)

सरल और समझने में आसान (Simple & Interpretable): Linear Regression जैसे मॉडल के परिणामों को समझना आसान है।
निरंतर मानों के लिए उपयोगी (Useful for Continuous Values): यह संख्यात्मक प्रेडिक्शन (Numerical Predictions) के लिए बेहतर है।
फीचर इम्पॉर्टेंस (Feature Importance): गुणांक (Coefficients) से पता चलता है कि कौन-से फीचर्स प्रेडिक्शन को प्रभावित करते हैं।

6. Regression की सीमाएं (Limitations)

लीनियर रिलेशनशिप की धारणा (Assumes Linear Relationship): अगर डेटा नॉन-लीनियर है, तो Linear Regression अच्छा परिणाम नहीं देता।
आउटलायर्स के प्रति संवेदनशील (Sensitive to Outliers): आउटलायर्स मॉडल के प्रदर्शन को खराब कर सकते हैं।
ओवरफिटिंग (Overfitting): Polynomial Regression जैसे कॉम्प्लेक्स मॉडल में ओवरफिटिंग की समस्या हो सकती है।

7. निष्कर्ष (Conclusion)

Regression मशीन लर्निंग का एक मूलभूत टूल है जो निरंतर मानों (Continuous Values) के प्रेडिक्शन के लिए उपयोगी है। यह सरल होने के साथ-साथ व्यापक रूप से लागू (Widely Applicable) है। हालांकि, डेटा के प्रकार (Type of Data) और समस्या (Problem) के अनुसार सही Regression टेक्निक चुनना महत्वपूर्ण है। Linear Regression से शुरुआत करके, आप नॉन-लीनियर समस्याओं के लिए Polynomial या Regularized Regression (Ridge/Lasso) का उपयोग कर सकते हैं।